Guia sobre funcionamento e aplicações de circuitos ressonantes RLC

Um circuito RLC é um circuito elétrico que consiste em um resistor, indutor e capacitor, eles são representados pelas letras R, L e C. Os circuitos RLC ressonantes são conectados em série e em paralelo. O nome circuito RLC é derivado da letra inicial dos componentes de resistência, indutor e capacitor. Para o propósito atual, o circuito forma um oscilador harmônico. Usando o Circuito LC ele ressoa. Se o resistor aumenta, ele decompõe as oscilações, é conhecido como amortecimento. Alguma resistência é difícil de encontrar em tempo real, mesmo depois que o resistor não é identificado como o componente, ele é resolvido pelo circuito LC.

Circuitos RLC Ressonantes

Ao lidar com o ressonante, ele é um componente complexo e tem muitas discrepâncias. A impedância z e seu circuito são definidos como

Z = R + JX

Onde R é a resistência, J é uma unidade imaginária e X é uma reatância.

Há um pulso assinado entre R e JX. A unidade imaginária é uma resistência externa. A energia armazenada são os componentes de o capacitor e indutor. Os capacitores são armazenados no campo elétrico e os indutores são armazenados no campo de magnitude.

COM_C= 1 / jωc

= -J / ωc

COM_eu= jωL

A partir da equação Z = R + JK, podemos definir as reatâncias como

X_C= -1 / ωc

X_{L =}ωL

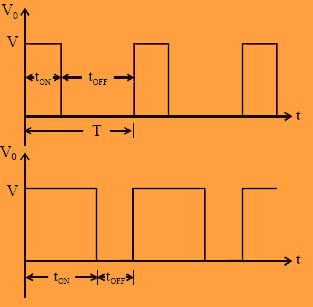
O valor absoluto da reatância de o indutor e carga do capacitor com frequência, conforme mostrado na figura abaixo.

Fator Q

A abreviatura do Q é definida como qualidade e também é conhecida como fator de qualidade. O fator de qualidade descreve o ressonador subamortecido. Se o ressonador subamortecido aumenta, o fator de qualidade diminui. O amortecimento do circuito ressonador elétrico gera a perda de energia nos componentes resistivos. A expressão matemática do fator Q é definida como o

Q ( ω ) = potência máxima energia armazenada / perda de potência

O fator q depende da frequência que é mais frequentemente citado para a frequência ressonante e a energia máxima armazenada no capacitor e no indutor pode calcular a frequência ressonante que é armazenada no circuito ressonante. As equações relevantes são

Energia máxima armazenada = LI^dois_Lrms= C V^dois_Crms

ILrms são indicados como a corrente RMS através do indutor. É igual à corrente RMS total formada no circuito em série e no circuito paralelo não é igual. Da mesma forma, no VCrms é uma tensão através do capacitor, ela é mostrada no circuito paralelo e é igual à tensão de alimentação rms, mas na série, o circuito é combinado por um divisor de potencial. Assim, o circuito em série é simples de calcular a energia máxima armazenada através de indicador e nos circuitos paralelos é considerada através de um capacitor.

O poder real degenera no resistor

P = V_Rrmseu_Rrms= Eu^dois_RrmsR = V^dois_Rrms/ R

A maneira mais fácil de encontrar o circuito RLC série

Q^(S)_ω0= ω₀ eu^dois_rmsL / I^dois_rmsR = ω₀L / R

O circuito paralelo deve considerar a tensão

Q^(P)_ω0= ω₀RCV^dois_Crms/ V^dois_Crms= ω₀CR

Circuito Série RLC

O circuito em série RLC consiste em resistência, indutor e capacitor que são conectados em série no circuito RLC em série. O diagrama abaixo mostra o circuito RLC em série. Neste circuito, o capacitor e o indutor irão se combinar e aumentar a frequência. Se pudermos reconectar o Xcis um negativo, então é claro que XL + XC deve ser igual a zero para esta frequência específica XL = -XCimpedância componentes do imaginário cancelam exatamente uns aos outros. Nesse movimento de frequência, a impedância do circuito tem baixa magnitude e ângulo de fase zero, sendo chamada de frequência ressonante do circuito.

Circuito Série RLC

X_eu+ X_C= 0

X_eu= - X_C= ω₀L = 1 / ω₀C = 1 / LC

ω_{0 =√1 / LC}ω₀

= 2Π f ₀

Circuito RLC Arbitrário

Podemos observar os efeitos de ressonância considerando a tensão entre os componentes resistivos e a tensão de entrada como um exemplo que podemos considerar para o capacitor.

VC / V = ​​1/1-ω^doisLC + j ωRC

Para os valores de R, L e C, a razão é traçada em relação à frequência angular e a figura mostra as propriedades de amplificação. Frequência de ressonância

VC / V- 1 / j ω₀RC

VC / V- j ω₀L / R

Podemos ver que por se tratar de um circuito positivo a quantidade total de potência dissipada é constante

Circuito RLC Paralelo

No circuito RLC paralelo, a resistência, o indutor e o capacitor do componente são conectados em paralelo. O circuito RLC ressonante é um circuito em série dupla nas funções de troca de tensão e corrente. Portanto, o circuito tem um ganho de corrente em vez da impedância e o ganho de tensão é máximo na frequência de ressonância ou minimizado. A impedância total do circuito é dada como

Circuito RLC paralelo

= R ‖ Z_eu‖ COM_C

= R / 1- JR (1 / X_C+ 1 / X_eu)

= R / 1+ JR (ωc - 1 / ωL)

Quando X_C = - X_eu Os picos ressonantes voltam e, portanto, a frequência ressonante tem a mesma relação.

ω_{0 =√1 / LC}

Para calcular o ganho de corrente olhando a corrente em cada um dos braços, o ganho do capacitor é dado como

eu_c/ i = jωRC / 1+ jR (ωc - 1 / ωL)

O ganho atual de magnitude é mostrado na figura e a frequência ressonante é

eu_c/ i = jRC

Aplicações dos circuitos ressonantes RLC

Os circuitos ressonantes RLC têm muitas aplicações como

• Circuito oscilador , receptores de rádio e aparelhos de televisão são usados ​​para fins de sintonia.
• O circuito em série e RLC envolve principalmente o processamento de sinal e sistema de comunicação
• O circuito LC ressonante série é usado para fornecer ampliação de tensão
• Circuito LC série e paralelo são usados ​​no aquecimento por indução

Este artigo fornece informações sobre o circuito RLC, os circuitos RLC em série e paralelos, o fator Q e as aplicações dos circuitos RLC ressonantes. Espero que as informações fornecidas no artigo sejam úteis para dar boas informações e compreender o projeto. Além disso, se você tiver alguma dúvida sobre este artigo ou sobre o projetos elétricos e eletrônicos você pode comentar na seção abaixo. Aqui está uma pergunta para você, no circuito RLC paralelo, qual valor pode sempre ser usado como uma referência de vetor?

Créditos fotográficos:

• Circuito Série RLC Sarutech
• Circuito RLC paralelo wikimedia