Nos circuitos combinacionais, portas lógicas diferentes são usadas para projetar codificador, multiplexador, decodificador e de-multiplexador. Esses circuitos têm algumas características como a saída deste circuito depende principalmente dos níveis que existem nos terminais de entrada a qualquer momento. Este circuito não inclui nenhuma memória. O estado anterior da entrada não tem qualquer influência no estado atual deste circuito. As entradas e saídas de um circuito combinacional são ‘n’ no. de entradas & ‘m’ não. de saídas. Alguns dos circuitos combinacionais são meio somador e somador completo, subtrator, codificador, decodificador, multiplexador e demultiplexador. Este artigo discute uma visão geral de meio somador e somador completo e está trabalhando com tabelas de verdade.

O que é um Adder?

Um somador é um circuito lógico digital na eletrônica, amplamente utilizada para a adição de números. Em muitos computadores e outros tipos de processadores, os somadores são usados até mesmo para calcular endereços e atividades relacionadas e calcular índices de tabela na ALU e até mesmo utilizados em outras partes dos processadores. Eles podem ser construídos para muitas representações numéricas como excesso-3 ou decimal codificado em binário. Os somadores são classificados basicamente em dois tipos: meio somador e somador completo.

O que é o circuito Half Adder e Full Adder?

O circuito meio somador tem duas entradas: A e B, que adicionam dois dígitos de entrada e geram um transporte e uma soma. O circuito somador completo tem três entradas: A e C, que somam três números de entrada e geram um transporte e uma soma. Este artigo fornece informações detalhadas sobre a finalidade de um meio somador e somador completo em formas tabulares e até mesmo em diagramas de circuito. Já foi mencionado que o propósito principal e crucial dos somadores é a adição. Abaixo estão os detalhados meio somador e teoria do somador completo.

Meio somador básico e somador completo

Meio somador

Então, chegando ao cenário de meio somador, ele adiciona dois dígitos binários onde os bits de entrada são denominados como augend e addend e o resultado será duas saídas, uma é a soma e a outra é o transporte. Para realizar a operação de soma, XOR é aplicado a ambas as entradas e a porta AND é aplicada a ambas as entradas para produzir o transporte.

Diagrama Funcional HA

Enquanto no circuito somador completo, ele adiciona 3 números de um bit, onde dois dos três bits podem ser referidos como operandos e o outro é denominado como bit transportado. A saída produzida é a saída de 2 bits e estes podem ser referidos para transportar e somar como saída.

Usando um meio somador, você pode projetar uma adição simples com a ajuda de portas lógicas.

Vejamos um exemplo de adição de dois bits únicos.

Os 2 bits meio somador tabela de verdade é como abaixo:

Mesa de verdade de meio somador

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10

Essas são as combinações de bit único menos possíveis. Mas o resultado para 1 + 1 é 10, o resultado da soma deve ser reescrito como uma saída de 2 bits. Assim, as equações podem ser escritas como

0 + 0 = 00
0 + 1 = 01
1 + 0 = 01
1 + 1 = 10

A saída '1' de '10' é carry-out. ‘SUM’ é a saída normal e ‘CARRY’ é o carry-out.

Agora foi esclarecido que um somador de 1 bit pode ser facilmente implementado com a ajuda do Gate XOR para a saída ‘SUM’ e um Gate AND para ‘Carry’.

Por exemplo, quando precisamos adicionar dois bytes de 8 bits juntos, ele pode ser implementado usando um circuito lógico somador completo. O meio somador é útil quando você deseja adicionar quantidades de um dígito binário.

Uma maneira de desenvolver somadores de dois dígitos binários seria fazer uma tabela verdade e reduzi-la. Quando você deseja fazer um somador de três dígitos binários, a operação de adição de meio somador é realizada duas vezes. Da mesma forma, quando você decide fazer um somador de quatro dígitos, a operação é realizada mais uma vez. Com essa teoria, ficou claro que a implementação é simples, mas o desenvolvimento é um processo demorado.

A expressão mais simples usa a função OU exclusiva:

Soma = A XOR B

Carry = A AND B

Diagrama Lógico HA

E uma expressão equivalente em termos de AND, OR e NOT básicos é:

SUM = A.B + A.B ’

Código VHDL para meio somador

Entidade ha é

Porta (a: em STD_LOGIC
b: em STD_LOGIC
sha: out STD_LOGIC
cha: out STD_LOGIC)
fim ha

A arquitetura comportamental do circuito acima é

começar
sha<= a xor b
não<= a and b
fim comportamental

Número IC de meio somador

A implementação de meio somador pode ser feita por meio de circuitos integrados de lógica digital CMOS de alta velocidade, como a série 74HCxx, que inclui o SN74HC08 (7408) e o SN74HC86 (7486).

Limitações de meio somador

A principal razão para chamar esses somadores binários como Metade somadores é que não há intervalo para incluir o bit de transporte usando um bit anterior. Portanto, esta é a principal limitação dos HAs uma vez usados como somadores binários, particularmente em situações de tempo real que envolvem a adição de vários bits. Portanto, essa limitação pode ser superada usando os somadores completos.

Full Adder

Este somador é difícil de implementar quando comparado ao meio somador.

Diagrama Funcional Completo do Somador

A diferença entre meio somador e somador completo é que o somador completo tem três entradas e duas saídas, enquanto meio somador tem apenas duas entradas e duas saídas. As duas primeiras entradas são A e B e a terceira entrada é uma entrada transportada como C-IN. Quando uma lógica de somador completo é projetada, você encadeia oito deles para criar um somador de todo o byte e cascata o bit de transporte de um somador para o próximo.

Tabela da verdade FA

O carry de saída é designado como C-OUT e a saída normal é representada como S, que é ‘SUM’.

Com o acima tabela de verdade de somador completa , a implementação de um circuito somador completo pode ser facilmente compreendida. O SUM 'S' é produzido em duas etapas:

Fazendo XOR nas entradas fornecidas 'A' e 'B'
O resultado de A XOR B é então XORed com o C-IN

Isso gera SUM e C-OUT é verdadeiro apenas quando duas das três entradas são HIGH, então o C-OUT será HIGH. Assim, podemos implementar um circuito de somador completo com a ajuda de dois circuitos de meio somador. Inicialmente, o meio somador será usado para adicionar A e B para produzir uma Soma parcial e uma lógica de somador do segundo semestre pode ser usada para adicionar C-IN à Soma produzida pelo somador do primeiro meio para obter a saída S final.

Se qualquer lógica do meio somador produzir um transporte, haverá um transporte de saída. Portanto, C-OUT será uma função OR das saídas Carry do meio somador. Dê uma olhada na implementação do circuito somador completo mostrado abaixo.

Diagrama Lógico Completo do Somador

“como um transistor funciona como um amplificador ”

A implementação de diagramas lógicos maiores é possível com a lógica do somador completo acima, um símbolo mais simples é usado principalmente para representar a operação. A seguir, é fornecida uma representação esquemática mais simples de um somador completo de um bit.

Com esse tipo de símbolo, podemos somar dois bits, obtendo um transporte da próxima ordem inferior de magnitude e enviando um transporte para a próxima ordem superior de magnitude. Em um computador, para uma operação de vários bits, cada bit deve ser representado por um somador completo e deve ser adicionado simultaneamente. Assim, para adicionar dois números de 8 bits, você precisará de 8 somadores completos, que podem ser formados pela cascata de dois dos blocos de 4 bits.

Half Adder e Full Adder usando K-Map

Mesmo as saídas de soma e transporte para meio somador também podem ser obtidas com o método do mapa de Karnaugh (K-map). O Expressão booleana de meio somador e somador total pode ser obtido através do K-map. Portanto, o K-map para esses somadores é discutido abaixo.

O meio somador K-map é

HA K-Map

O somador K-Map completo é

FA K-Map

Expressão Lógica de SUM e Carry

A expressão lógica de soma (S) pode ser determinada com base nas entradas mencionadas na tabela.

= A’B’Cin + A ’B CCin’ + A B’Cin ’+ AB Cin
= Cin (A’B ’+ AB) + Cin’ (A’B + A B ’)
= Cin EX-OR (A EX-OR B)
= (1,2,4,7)

A expressão lógica do carry (Cout) pode ser determinada com base nas entradas mencionadas na tabela.

= A’B Cin + AB’Cin + AB Cin ’+ ABCin
= AB + BCin + ACin
= (3, 5, 6, 7)

Com as tabelas de verdade mencionadas acima, os resultados podem ser obtidos e o procedimento é:

Um circuito combinacional combina as diferentes portas do circuito onde essas podem ser um codificador, decodificador, multiplexador e demultiplexador . As características dos circuitos combinacionais são as seguintes.

A saída em qualquer instante de tempo é baseada apenas nos níveis que estão presentes nos terminais de entrada.
Ele não usa nenhuma memória. O estado anterior da entrada não tem nenhum efeito no estado atual do circuito.
Ele pode ter qualquer número de entradas em número de saídas.

Codificação VHDL

Codificação VHDL para somador completo inclui o seguinte.

entidade full_add é

Porta (a: em STD_LOGIC
b: em STD_LOGIC
cin: em STD_LOGIC
soma: fora STD_LOGIC
cout: out STD_LOGIC)
fim full_add

“o que é um sensor óptico ”

O comportamento da arquitetura de full_add é

componente ha é
Porta (a: em STD_LOGIC
b: em STD_LOGIC
sha: out STD_LOGIC
cha: out STD_LOGIC)
componente final
sinal s_s, c1, c2: STD_LOGIC
começar
HA1: mapa da porta ha (a, b, s_s, c1)
HA2: mapa da porta ha (s_s, cin, sum, c2)
custo<=c1 or c2
fim comportamental

O diferença entre meio somador e somador completo é que meio somador produz resultados e somador completo usa meio somador para produzir algum outro resultado. Da mesma forma, enquanto o Full-Adder é de dois Half-Adders, o Full-Adder é o bloco real que usamos para criar os circuitos aritméticos.

Carry Lookahead Adders

No conceito de circuitos somadores de transporte de ondulação, os bits necessários para a adição estão imediatamente disponíveis. Considerando que cada seção de somador precisa reter seu tempo para a chegada do transporte do bloco de somador anterior. Por causa disso, leva mais tempo para produzir SUM e CARRY, pois cada seção no circuito espera pela chegada da entrada.

Por exemplo, para entregar a saída para o enésimo bloco, ele precisa receber a entrada do (n-1) o bloco. E esse atraso é correspondentemente denominado como atraso de propagação.

Para superar o atraso no somador de transporte de ondulação, um somador de transporte antecipado foi introduzido. Aqui, usando hardware complicado, o atraso de propagação pode ser minimizado. O diagrama a seguir mostra um somador carry lookahead usando somadores completos.

Realizar lookahead usando Full Adder

A tabela verdade e as equações de saída correspondentes são

PARA	B	C	C + 1	Doença
0	0	0	0	Sem transporte Gerar
0	0	1	0
0	1	0	0
0	1	1	1	Sem transporte Propagar
1	0	0	0
1	0	1	1
1	1	0	1	Carregar Gerar
1	1	1	1	Carregar Gerar

A equação de propagação de transporte é Pi = Ai XOR Bi e a geração de transporte é Gi = Ai * Bi. Com essas equações, as equações de soma e transporte podem ser representadas como

SUM = Pi XOR Ci

Ci + 1 = Gi + Pi * Ci

Gi entrega transporte somente quando ambas as entradas Ai e Bi são 1 sem considerar o transporte de entrada. Pi está relacionado à propagação de transporte de Ci para Ci + 1.

Diferença entre Half Adder e Full Adder

O diferença entre a meia soma e a tabela de soma completa é mostrado abaixo.

Meio somador	Full Adder
Half Adder (HA) é um circuito lógico combinacional e este circuito é usado para adicionar dois dígitos de um bit.	Full Adder (FA) é um circuito combinacional e este circuito é usado para adicionar três dígitos de um bit.
Em HA, uma vez que o transporte é gerado a partir da adição anterior, não pode ser adicionado à próxima etapa.	No FA, uma vez que o transporte é gerado a partir da adição anterior, ele pode ser adicionado à próxima etapa.
O meio somador inclui duas portas lógicas como porta AND e porta EX-OR.	O somador completo inclui duas portas EX-OR, duas portas OR e duas portas AND.
Os bits de entrada no meio somador são dois como A, B.	Os bits de entrada no somador completo são três, como A, B e C-in
Metade soma soma e equação de transporte é S = a⊕b C = a * b	A expressão lógica do somador completo é S = a ⊕ b⊕Cin Cout = (a * b) + (Cin * (a⊕b)).
HA é usado em computadores, calculadoras, dispositivos usados para medição digital, etc.	FA é usado em processadores digitais, adição de múltiplos bits, etc.

O principais diferenças entre meio somador e somador completo são discutidos abaixo.

Metade somador gera soma e transporte adicionando duas entradas binárias enquanto o somador completo é usado para gerar soma e transporte adicionando três entradas binárias. Ambas as arquiteturas de hardware meio somador e somador total não são iguais.
A principal característica que diferencia HA e FA é que em HA não existe tal acordo para considerar o último carregamento de adição como sua entrada. Mas, um FA localiza uma coluna de entrada particular como Cin para considerar o carry da última adição.
Os dois somadores apresentarão uma diferença com base nos componentes usados no circuito para sua construção. Os meios somadores (HA's) são projetados com a combinação de duas portas lógicas como AND e EX-OR, enquanto o FA é projetado com a combinação de três portas AND, duas XOR e uma OR.
Basicamente, os HA operam em 2 ou duas entradas de 1 bit, enquanto os FA operam em três entradas de 1 bit. O meio somador é usado em diferentes dispositivos eletrônicos para avaliar a adição, enquanto o somador completo é usado em processadores digitais para a adição de um bit longo.
As semelhanças entre esses dois somadores são: HA e FA são circuitos digitais combinacionais, portanto, eles não usam nenhum elemento de memória, como circuitos sequenciais. Esses circuitos são essenciais para a operação aritmética para fornecer a adição do número binário.

Implementação Full Adder usando Metade Adders

A implementação de um FA pode ser feita por meio de dois meios somadores que estão conectados logicamente. O diagrama de blocos disso pode ser mostrado abaixo, que informa a conexão de um FA usando dois meios somadores.
A soma e as equações de transporte de cálculos anteriores são

S = A ‘B’ Cin + A ’BC’ em + ABCin

Cout = AB + ACin + BCin

A equação da soma pode ser escrita como.

Cin (A’B ‘+ AB) + C‘ in (A’B + A B ’)

Então, Soma = Cin EX-OR (A EX-OR B)

Cin (A EX-OR B) + C’in (A EX-OR B)

= Cin EX-OR (A EX-OR B)

Cout pode ser escrito da seguinte forma.

COUT = AB + ACin + BCin.

Cout = AB + + desilusões BCIN (A + A)

= ABCin + AB + ACin + A ’B Cin

= AB (1 + Cin) + ACin + A ’B Cin

= A B + ACin + A ’B Cin

= AB + ACin (B + B ’) + A’ B Cin

= ABCin + AB + A’B Cin + A ’B Cin

= AB (Cin + 1) + A B Cin + A ’B Cin

= AB + AB ’Cin + A’ B Cin

= AB + Cin (AB ’+ A’B)

Portanto, COUT = AB + Cin (A EX-OR B)

Dependendo das duas somas e equações de transporte acima, o circuito FA pode ser implementado com a ajuda de dois HAs e uma porta OR. O diagrama de circuito de um somador completo com dois meio somadores é ilustrado acima.

Full Adder usando dois meios somadores

Design Full Adder com o uso de portas NAND

Uma porta NAND é um tipo de porta universal, usada para executar qualquer tipo de projeto lógico. O circuito FA com o diagrama de portas NAND é mostrado abaixo.

FA usando portas NAND

FA é um somador de um bit fácil e se desejarmos executar a adição de n bits, então n não. de FAs de um bit devem ser empregados no formato de conexão em cascata.

Vantagens

O vantagens de meio somador e somador completo inclui o seguinte.

O objetivo principal de um meio somador é adicionar dois números de bit único
Os somadores completos têm a capacidade de adicionar um bit de transporte que é o resultado da adição anterior
Com o somador completo, circuitos cruciais como somador, multiplexador e muitos outros podem ser implementados
Os circuitos somadores completos consomem energia mínima
As vantagens de um somador completo em relação a meio somador são: um somador completo é usado para superar a desvantagem de um meio somador porque meio somador é usado principalmente para adicionar dois números de 1 bit. Metade adicionadores não adicionam o carry bit, então, para superar, este adicionador completo é empregado. No somador completo, a adição de três bits pode ser feita e gera duas saídas.
O projeto de somadores é simples e é um bloco de construção básico para que a adição de um bit possa ser facilmente compreendida.
Este somador pode ser convertido em meio subtrator adicionando um inversor.
Usando um somador completo, alto rendimento pode ser obtido.
Alta velocidade
Muito forte para fornecer escala de tensão

Desvantagens

O desvantagens de meio somador e somador completo inclui o seguinte.

Além disso, meio somador não pode ser usado antes de carregar, portanto, não é aplicável para adicionar em cascata de vários bits.
Para superar esta desvantagem, FA é necessário adicionar três 1 bit.
Uma vez que o FA é usado na forma de uma cadeia como um RA (Ripple Adder), então a capacidade de saída do drive pode ser diminuída.

Formulários

As aplicações de meio somador e somador completo incluem o seguinte.

A adição de bits binários pode ser feita por meio somador usando ALU dentro do computador porque ele usa somador.
A combinação de meio somador pode ser usada para projetar um circuito de somador completo.
Metade somadores são usados nas calculadoras e para medir os endereços, bem como as tabelas
Esses circuitos são usados para lidar com diferentes aplicações em circuitos digitais. No futuro, ele terá um papel fundamental na eletrônica digital.
Um circuito FA é usado como um elemento em muitos circuitos grandes, como o Ripple Carry Adder. Este somador adiciona o número de bits simultaneamente.
FAs são usados na Unidade Lógica Aritmética (ALU)
FAs são usados em aplicativos relacionados a gráficos como GPU (Unidade de processamento gráfico)
Eles são usados no circuito de multiplicação para executar a Multiplicação de realização.
Em um computador, para gerar o endereço de memória e construir o contraponto do programa para a instrução subsequente, a Unidade Lógica Aritmética é usada usando Somadores Completos.

Assim, sempre que a adição de dois números binários é feita, os dígitos são adicionados primeiro pelos menos bits. Este processo pode ser realizado por meio de um meio somador, pois o mais simples n / w permite somar dois números de 1 bit. As entradas deste somador são os dígitos binários, enquanto as saídas são a soma (S) e o transporte (C).

Sempre que o número de dígitos é incluído, a rede HA é utilizada simplesmente para conectar o mínimo de dígitos, já que o HA não pode adicionar o número de transporte da classe anterior. Um somador completo pode ser definido como a base de todos os dispositivos aritméticos digitais. Isso é usado para adicionar três números de 1 dígito. Este somador inclui três entradas como A, B e Cin, enquanto as saídas são Soma e Cout.

Conceitos Relacionados

O conceitos relacionados a meio somador e somador completo apenas não se atenha a um único propósito. Eles têm uso extensivo em muitos aplicativos e alguns dos relacionados são mencionados:

Número IC de meio somador e somador completo
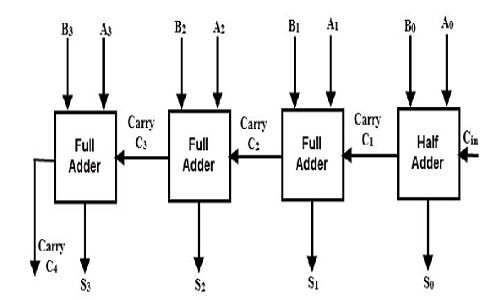
Desenvolvimento de somador de 8 bits
Quais são as precauções de meio somador?
Applet JAVA de um Ripple Carry Adder

Portanto, isso é tudo sobre o teoria de meio somador e somador total junto com as tabelas de verdade e diagramas lógicos, o projeto de somador completo usando circuito de meio somador também é mostrado. Muitos dos meio somador e somador completo em pdf documentos estão disponíveis para fornecer informações avançadas sobre esses conceitos. Além disso, é importante saber como um somador completo de 4 bits é implementado ?