Uma configuração na qual um transistor de junção bipolar ou um BJT é reforçado com um resistor de emissor para aumentar sua estabilidade em relação às mudanças de temperatura ambiente, é chamada de circuito polarizado de emissor estabilizado para BJT.
Já estudamos o que é Polarização DC em transistores , agora vamos seguir em frente e aprender como um resistor de emissor pode ser usado para melhorar a estabilidade de uma rede de polarização BJT DC.
Aplicando Circuito de Polarização Estabilizado de Emissor
A inclusão do resistor do emissor na polarização CC do BJT oferece estabilidade superior, ou seja, as correntes e tensões de polarização contínua continuam mais próximas de onde foram fixadas pelo circuito considerando parâmetros externos, como variações de temperatura, e transistor beta (ganho),
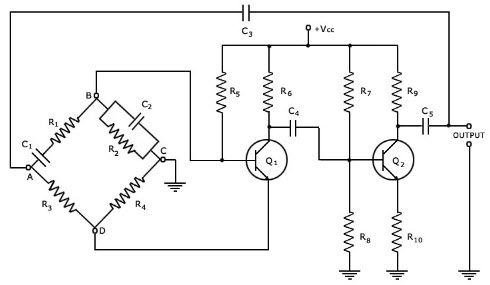
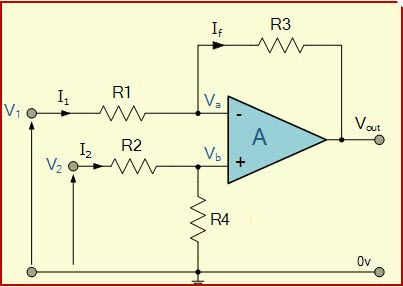
A figura abaixo mostra uma rede de polarização de transistor DC tendo um resistor de emissor para impor uma polarização de emissor estabilizado na configuração de polarização fixa existente do BJT.

Figura 4.17 Circuito de polarização BJT com resistor de emissor
Em nossas discussões, começaremos nossa análise do projeto inspecionando primeiro o loop ao redor da região base-emissora do circuito e, em seguida, usaremos os resultados para investigar mais profundamente o loop ao redor do lado coletor-emissor do circuito.
Loop do emissor de base

Podemos redesenhar o loop base-emissor acima da maneira mostrada abaixo na Fig 4.18, e se aplicarmos Lei de tensão de Kirchhoff neste loop no sentido horário, nos ajuda a obter a seguinte equação:
+ Vcc = IBRB - VBE - IERE = 0 ------- (4.15)
De nossas discussões anteriores, sabemos que: IE = (β + 1) B ------- (4.16)
Substituir o valor de IE na Eq. (4.15) fornece o seguinte resultado:
Vcc = IBRB - VBE - (β + 1) IBRE = 0
Colocar os termos em seus respectivos grupos resulta no seguinte:

Se você se lembra de nossos capítulos anteriores, a equação de polarização fixa foi derivada da seguinte forma:

Se compararmos esta equação de polarização fixa com a equação (4.17), encontramos que a única diferença entre as duas equações para o IB atual é o termo (β + 1) RE.
Quando a equação 4.17 é usada para desenhar uma configuração baseada em série, podemos extrair um resultado interessante, que na verdade é semelhante à equação 4.17.

Veja o exemplo da seguinte rede na Fig 4.19:
Se resolvermos o sistema para o IB atual, resulta na mesma equação obtida na Eq. 4,17. Observe que além da tensão da base ao emissor VBE, o resistor RE pode ser visto aparecendo novamente na entrada do circuito base por um nível (β + 1).
Ou seja, o resistor do emissor que faz parte do circuito coletor-emissor aparece como (β + 1) RE no loop base-emissor.
Supondo que β possa estar principalmente acima de 50 para a maioria dos BJTs, o resistor no emissor dos transistores pode ser significativamente maior no circuito base. Portanto, somos capazes de derivar a seguinte equação geral para a Fig.4.20:
Ri = (β + 1) RE ------ (4,18)
Você achará esta equação bastante útil ao resolver muitas redes futuras. Na verdade, essa equação facilita a memorização da equação 4.17.
De acordo com a lei de Ohm, sabemos que a corrente em uma rede é a tensão dividida pela resistência do circuito.
A tensão para um projeto de emissor de base é = Vcc - VBE
As resistências vistas no 4.17 são RB + RE , que é refletido como (β + 1), e o resultado é o que temos na Eq 4.17.
Loop Coletor-Emissor

A figura acima mostra o loop coletor-emissor, aplicando Lei de Kirchhoff para o loop indicado no sentido horário, obtemos a seguinte equação:
+ ONTEM + VCE + CICV - VCC = 0


Resolvendo um exemplo prático para um circuito de polarização estabilizado por emissor, conforme dado abaixo:
Para a rede de polarização do emissor, conforme apresentado na figura 4.22 acima, avalie o seguinte:
- IB
- IC
- VCE
- VC
- E
- ETC
- VBC

Determinando o nível de saturação

A corrente máxima do coletor que se torna o coletor nível de saturação para uma rede de polarização de emissor poderia ser calculada empregando a estratégia idêntica que havia sido aplicada para nosso circuito de polarização fixa .

Ele pode ser implementado criando um curto-circuito através do coletor e do emissor do BJT, conforme indicado no diagrama 4.23 acima, e então podemos avaliar a corrente do coletor resultante usando a seguinte fórmula:
Exemplo de problema para resolver a corrente de saturação em um circuito BJT estabilizado por emissor:


Análise de linha de carga
A análise da linha de carga do circuito BJT de polarização do emissor é bastante semelhante à nossa configuração de polarização fixa discutida anteriormente.
A única diferença sendo o nível de IB [conforme derivado em nossa Eq. (4.17)] define o nível de IB nas características conforme mostrado na Fig. 4.24 a seguir (indicado como IBQ).

Anterior: Análise da Linha de Carga em Circuitos BJT Próximo: Polarização do divisor de tensão em circuitos BJT - mais estabilidade sem fator beta